One of the most important task in deep learning is classification. This involves predicting the class to which a given input data belongs. Models such as convolution neural networks (CNN) and Large language models use classification layers. These models produce output predictions for all possible classes, but these predictions are not immediately usable as they can be any floating point number. The softmax function is essential in converting these raw model outputs, known as logits, into probabilities that sum to one, making them interpretable

The role of Softmax in Classification#

Why softmax?#

Raw model outputs, or logits can lie anywhere within the floating-point number range, making them difficult to interpret. The Softmax function addresses this by normalizing the logits into a probability distribution. This allows us to understand the model’s confidence in its predictions.

Steps to calculate Sofmax#

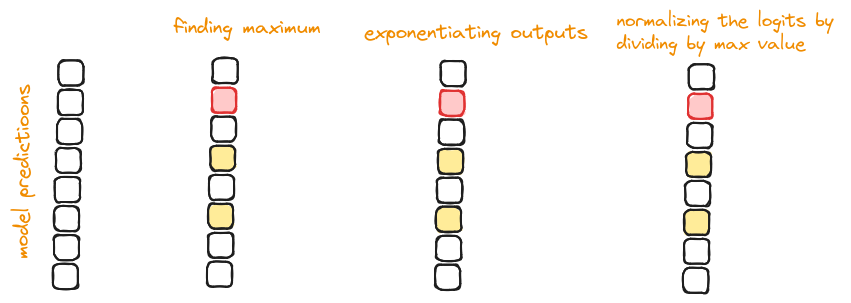
1. Normalizing by maximum logit:

   • The first step involves calculating the maximum value among the model’s outputs. This helps in normalizing the outputs and prevents potential overflow issues during exponentiation.

2. Exponentiation:

   • Next we subtract the maximum logit from each logit and calculate the exponent of these normalized values. This step transforms the logits into a form where they can be compared proportionally.

3. Division by sum of exponents:

   • Finally we divide each exponentiated value by the sum of all exponentiated values. This step ensures that the resulting probabilities sum to one, providing a valid probability distribution.

import torch

def softmax(x):
    """Compute softmax values for each set of scores in x."""
    if not isinstance(x, torch.Tensor):
        x = torch.tensor(x, dtype=torch.float32)

    x_max = x.max(dim=-1, keepdim=True).values
    e_x = torch.exp(x - x_max)

    return e_x / e_x.sum(dim=-1, keepdim=True)

# Example usage
input_tensor = torch.tensor([1.0, 2.0, 3.0])
softmax_output = softmax(input_tensor)
print(softmax_output)

As we can see, the standard Softmax algorithm has some drawbacks. One significant issue is that it requires multiple passes over the entire tensor to calculate the softmax, makind it less cache-friendly and potentially inefficient.

Introducing Online Softmax#

To address these inefficiencies, we can explore an alternative approach known as online softmax. This method aims to improve computational efficiency and cache performance by processing the data in a more streamlined manner.

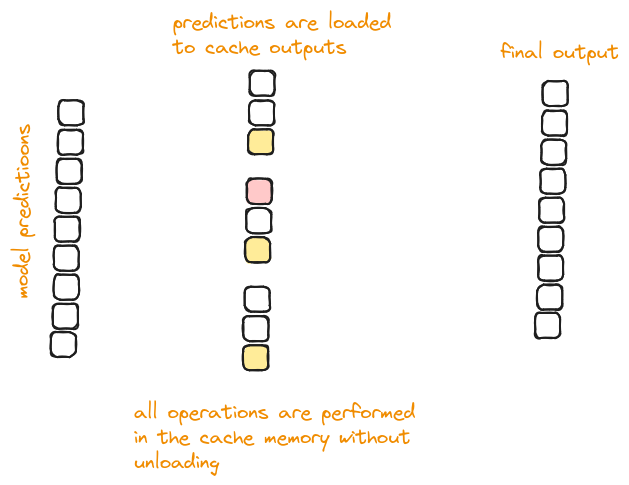
1. Single pass for maximum and sum calculation:

   • Instead of first finding the maximum value in one pass and then computing the sum of exponentials in another, this code combines these operation. When a new maximum value is found the sum is adjusted accordingly, ensuring accuracy without additional passes.

2. Numerical Stability

   • By subtracting the maximum value maxval from each element before exponentiation, the code prevents potential overflow issues that could occur with large input values.

3. Efficiency:

   • This approach is more cache-friendly as it reduces the number of passes over the data, thus maximising the number of times the data needs to be fetched from memory.

{#include <math.h>
#include <float.h>  // For FLT_MAX

void softmax_online(const float *input, float *output, int n) {
    float max_val = -INFINITY;
    float sum = 0.0f;
    for (int i = 0; i < n; i++) {
        float maxval_prev = max_val;
        if (inp_row[j] > max_val) {
            max_val = inp_row[j];
            sum = sum + expf(maxval_prev - max_val) + expf(inp_row[j] - max_val);
        } else {
            sum += expf(inp_row[j] - max_val);
        }
    }
    for (int i=0; i<n; i++) {
        output[i] = expf(inp_row[i] - max_val) / sum;
    }
}

template <typename T>
__global__
void softmax_kernel_v2(T* qk_buf_, /*const T* attr_mask, */const int batch_size, const int head_num,
  const int seq_len, const T scaler)
{
    // int batch_id = blockIdx.x / head_num / seq_len;
    // int seq_id = blockIdx.x % seq_len;
    int qk_offset = blockIdx.x * seq_len;
    // int mask_offset = batch_id * seq_len * seq_len + seq_id * seq_len;

    __shared__ float s_sum, s_max;

    float qk = threadIdx.x < seq_len ? (float)qk_buf_[threadIdx.x + qk_offset] : 0.0f;
    // float mask_val = threadIdx.x < seq_len ? (float)attr_mask[threadIdx.x + mask_offset] : 0.0f;

    // mask_val = (1.0f - mask_val) * -10000.0f;

    // float tmp = threadIdx.x < seq_len ? (float)(qk * (float)scaler + mask_val) : -1e20f;
    float tmp = -1e20f;
    float max_val = blockReduceMax<float>(tmp);
    if(threadIdx.x == 0)
      s_max = max_val;
    __syncthreads();

    float qk_tmp = threadIdx.x < seq_len ? __expf((float)(tmp - s_max)) : 0.0f;
    float sum_val = blockReduceSum<float>(qk_tmp);

    if(threadIdx.x == 0)
    {
      s_sum = sum_val + 1e-6f;
    }
    __syncthreads();

    if(threadIdx.x < seq_len)
      qk_buf_[threadIdx.x + qk_offset] = (T)(qk_tmp / s_sum);
}

This code becomes even more efficient when used on GPU’s as all tensor data can be moved to GPU’s shared memory

References#

• Online normalizer calculation for softmax Paper